项目主持：尹晓红
项目团队：尹晓红 李泳鲜 夏文俊 孟国连
（1） 研究背景和意义
轨迹跟踪控制是移动机器人研究的基础性问题，是智能化技术的核心，因此提高WMR 的轨迹跟踪控制性能对于提高 WMR 自动化水平具有重要的理论意义和实用价值。然而，当WMR存在初始位姿误差或参考轨迹不连续时，传统的控制方法会产生一个较大初始速度跳变，而这在现实中是不可实现的；另外，很多控制方法都是在理想速度成立的假设基础上进行的，所以当进行实际轨迹跟踪时，小车会产生较大的跟踪误差且鲁棒性不够理想。目前虽然神经网络已经广泛应用于各种控制领域，但是所研究的神经网络主要还是属于统计物理学范畴，对微观的生物神经动力学的研究还很少。现有的人工神经网络中的基本元件——神经元仅具有生物神经元的某些特性，有些甚至不考虑其内部的离子通道机制，与生物神经元的真实情况相差甚远。随着美国学者Walter J. Freeman教授的著作《神经动力学——对介观脑动力学的探索》的问世，神经科学引起了科学界重视。我们知道，大脑之所以能够处理极其复杂的分析和推理工作，一方面是因为其神经元个数的庞大（最近几年的研究结果认为人脑的神经元数量为1013），另一方面还在于神经元对输入信号的非线性处理能力。人们若想对各类脑神经过程获得系统的理解，就需要建立并发展一个有效的数学模型。
尹晓红博士主持的国家自然科学基金理论物理专项“基于生物神经动力学的轮式移动机器人轨迹跟踪控制研究（11247273）”专门针对这类问题开展研究。该项目研究生物神经动力学机制，建立生物神经动力学模型，采用基于神经动力学的方法来解决非完整WMR跟踪控制或一般非线性系统控制中的实际问题，实现更有效地WMR智能控制。
（2）神经动力学数学模型
门限偶极子模型是一种典型的神经动力学模型，如图2所示，门限偶极子模型由on和off两个相反信道组成，on信道接收来自目标神经元和邻居神经元的激励输入信号J；off信道接收来自障碍物的抑制输入信号K。两信道同时受唤醒输入信号I影响。其中激励输入信号J和抑制输入信号K分别为：
；
式中M为与第i个神经元相邻的神经元个数；Ii为第i个神经元的外部输入信号：Ii=E（目标处）；-E（障碍处）；0（自由空间），其中E是远大于上限B（B的引出见下文）的正常数，即E
B。非线性超阈值函数[xj]+=max{xj, 0}，[xj]-=max{-xj, 0}；wij为第i和第j个神经元间的连接权重，它是关于距离的递减函数，定义为：wij= f(dij)=μ/ dij (dij
r0)或0(dij>r0)，其中dij为第i、j个神经元间空间位置的欧氏距离；
和
为正常数。
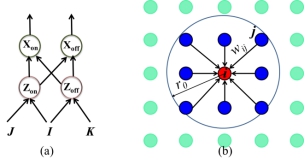
图2 神经动力学模型：（a）门限偶极子模型和（b）神经元邻接图
生物激励动态神经网络中第i个神经元的动态特性为：
(1)
式中，A为被动衰减率，B和D分别为第i个神经元
活动状态的上下限，参数A、B和D均为正常数。
变送器
和
的动态特性为：
(2)
(3)
式中参数
、
、
均为正常数,
、
分别表示变送器的生成速率和衰减速率，
表示变送器总量。
（3）神经元的光滑特性研究
以下对该门限偶极子模型的输出光滑特性进行简略分析。设第i个神经元初始状态xi=0，当0<t£4时抑制信号输入K为0，当4<t<8时 激励信号输入J为0。取参数A= 5，B=D= 2。在不同激励和抑制输入信号下，神经元的状态输出动态变化过程如图3所示。由该图可知，在参数A、B和D确定的情况下，输出信号的动态响应主要和激励输入J和抑制输入K有关，输出信号的幅值随着输入信号的增大而增大，但并非呈线性关系。而且由图3可知不论输入信号如何取值，神经元的状态输出总是位于有界区域[-D，B]内，即状态输出信号是光滑且有界的。因此，此模型具有稳定和输出光滑有界等优良特性，能有效抑制信号的跳变问题。经过此模型滤波后的信号比较柔和，可明显改善控制器的鲁棒性。
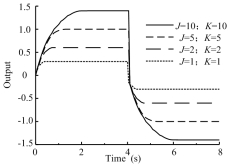
图3 生物伸进元光滑特性
本项目主要研究生物神经网络中的神经元在神经信息学中的起的作用，并将之应用到移动机器人运动中，实现移动机器人的鲁棒控制。
（4）生物神经动力学的在非完整WMR系统中的应用研究
以具有非完整约束的三轮WMR为研究对象（如图4所示），该WMR具有一个驱动/转向前轮及两个支撑后轮。图中，d表示WMR质心C至车后轴中心点的距离。设WMR的当前实际位姿状态为X=[x y θ]T，任意给定的参考位姿状态为Xr=[xryrθr]T，位姿误差为Xe=[xeyeθe]T，WMR当前实际速度矢量为U=[v ω]T, 任意给定的参考速度矢量Ur=[vrωr]T，其中v和ω分别表示WMR车架的线速度和角速度。非完整约束（即
）的存在说明WMR只能作纯滚无滑运动。
图4 WMR结构示意图
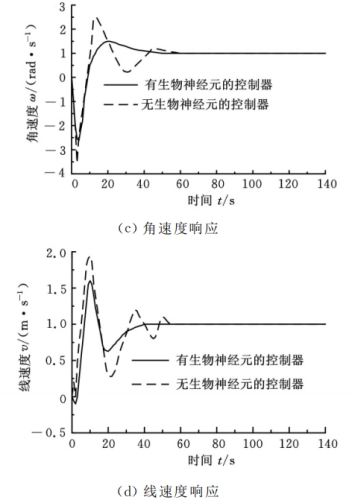
初始速度跳变问题往往会被研究者忽视。在常规的轨迹跟踪控制器作用下，控制系统往往会出现初速度跳变的情况，即当ｔ＝０时，ＡＧＶ的速度往往会突变到一个很大的值，而这在现实系统中是不可实现的。基于生物神经动力学的控制算法有效地弥补了这一缺点，从图5可以看出，利用本文设计的基于生物激励神经动力学系统的轨迹跟踪控制律进行跟踪控制，跟踪路径平滑、跟踪快、速度平稳。由图5c和图5d可以看出，用此控制律去跟踪AGV小车可有效减小初始速度的跳变，小车的输出有界、柔和，从而能实现安全有效的控制。
（5）部分控制结果图
